7月8日在《美国国家科学院院刊》（PNAS）发表了名为《空气污染对预期寿命的长期影响：基于中国淮河取暖分界线的证据》一文。这篇文章指出，冬季燃煤取暖的政策导致悬浮颗粒物浓度增加，进而导致淮河以北人均寿命寿命降低了5.5年；进一步的，作者认为，这导致整个北方5亿人损失了超过25亿年的人均寿命。这一结论引起了国内外媒体的广泛关注。

然而，我们认为该文的方法和结论都有很多可以商榷之处。本文将首先介绍该文使用的计量研究方法Regression Discontinuity Design (RDD)，然后来讨论作者对于人均寿命损失的估计是否有偏误，以及作者是否可以外推淮河两岸的结论到整个北方地区。对计量方法不感兴趣的读者可以直接跳到第三部分，看看我为什么不同意作者的结论。

一、自然实验与RDD

假设我们要研究北京大学对我终生收入的影响，应该怎么研究？

最直接的办法就是把北大人的平均工资和非北大人的平均工资相减。大家可能立即就能看出这个方法不靠谱的地方。除了教育以外，还有许多其他潜在因素也会影响收入，例如个人的智商、情商，父母的教育水平等等。很难相信北大人在这些变量上和非北大人的分布是一模一样的。

 如果社会科学可以像自然科学那样做可控实验，那么这个问题可以迎刃而解。首先，创造另一个“我”。这个“我”在其他各方面都和现实世界的“我”一样；唯一的区别就是现实世界的我去了北大，而假想“我”去了浙大。快进50年，等我们两个都入土的时候，看一生收入的差别。用数学语言来讲，假设终生收入是Y【这是个随机变量】，D是有没有上没上北大，X是其他所有混淆变量。在我们的理想实验中，其他变量都被控制为相同，因此X完全相同，所以我们通过这个理想实验来估算

政策效果 = E(Y|D=1, X) - E(Y|D=0, X)

当然，现实世界中，这样的实验是不可能存在的。那么我们应该怎么做呢？

 正如之前所说，我们做实验的目的就是控制其他混淆变量，所以如果我们能找出所有的X，并找到它们影响Y的方程形式Y = f(X, D)，那么即使不做这个实验，我们也可以通过函数拟合来估计，这种办法被称为结构模型。

政策效果 = f(D=1, X) - f(D=0, X)

回到之前的北大对于收入的影响，我们可以把所有变量（X）和是否上北大（D）都放进线性回归（OLS）中去拟合。D系数的估计值就是“控制住”其他变量后，上北大对于一个人收入的影响。这种办法的问题在于，找到所有X几乎是不可能的，确定它们对Y的函数形式更是难上加难。以OLS为例，这些变量是不是全部相关变量，它们到底是不是线性组合，那就只有天知道了。

 因为结构模型的这些问题，计量经济学界越来越倾向于使用自然实验的方法来研究这些问题；而RDD是自然实验中方法中的的一个分支。说到底，RDD做了一个假设，那就是在一个小范围内（间断点【discontinuity】附近），混淆变量的分布在受试组和控制组中一样的[1]；而D的分布则天差地别[2]。因此，我们可以用以下的方法来近似真实政策效果

政策效果 = Y|D=1 - Y|D=0

在之前的北大的例子中，我们可以假设，北大浙江分数线上下10分的孩子的其他变量是同分布的；他们上没上线更多地是临场发挥运气，而非他们智商、情商或者拼爹拼娘的结果。这样一群混淆变量分布相同的孩子，因为北大有条硬分数线而被“随机”分成了上了北大（D=1）和没上北大（D=0）两个人群。那么，通过比较这两个人群的终生收入，我们就可以估计北大对于个人收入的影响。如果这个假设是正确的，那么这个估计就是无偏的（unbiased）。

二、RDD的软肋

你现在可能有两个问题：

（1）为什么你可以假设分数线上下的孩子的混淆变量是同分布的？

（2）为什么你把比较组划定在上下10分的群体，而不是上下1分或者20分？

 这两个问题正是RDD的软肋。

关于同分布的假设。这个玩意没有办法严格证明，你信就是信，不信就是不信。作者可以做的事情有两件：第一是做大量的讨论，向读者证明，凡是你能想到的区别，我们都想到了，凡是你没想到的区别，我们也想到了。即便如此，我们的结论也是成立的。第二是控制已有变量。利用已有变量的多次项拟合来近似非线性方程，并且试用不同的多次项来证明文章的结果对于具体的方程形式免疫（i.e. robust）。但这并不是免死金牌，因为即使你证明已知变量对于估计结果没有影响，但是未知变量你还是没有控制，而是通过假设把它们消去了。

关于比较组边界的划定，这里有个偏误与标准误的取舍（trade off）。

先说为什么把边界划在10分，而不是20分。因为我们会担心，高考相距40分已经不能简单用运气来解释了，而是需要用实力来解释。不论是他们智商高，还是情商高，总之他们不一样。当他们不一样时，特别是未知变量不一样时，RDD的根本假设就分崩离析，RDD的估计值就会有偏误。例如，线上20分的学生比线下20分的学生情商要高，这些情商会导致年工资增加1万元；如果模型中没有情商一项，那么我们就会把这1万元的差异错误地归结为北大的正面影响，从而高估了上北大的作用，造成统计量的系统性偏误（bias）。由于RDD对于边界外的估计完全没有发言权，因此RDD的估计量是一个区间估计量（Local Average Treatment Effect），无法外推导总体性质。总而言之，为了降低偏误，划界时应该尽可能的靠近间断点。

既然要靠近间断点，为什么不把边界划在1分上下呢？这主要是考虑到样本量大小的问题。如果样本量太小，随机因素的干扰就太强，估计值的精度就太低，实际意义也不大。例如，我可能得出北大对于工资影响的点估计是年均10万元，但是标准误也是10万元；那么95%的置信区间里，北大既有可能帮倒忙（左端点大约是负10万元）也有可能帮大忙（右端点大约是30万元）：等于什么也没说。因此，为了降低标准误（standard error），划界时不应太靠近间断点。

由于偏误和标准误的取舍是一个艺术问题而不是一个技术问题，因此，一般好的RDD文章都会报告使用不同的边界值后得出的结果，如果结果定性结论不变，那么这个就是靠谱的。

当然，这只是对于RDD的粗浅介绍。RDD还有许多具体细节，如果大家有兴趣，可以去看Imbens的神文Regression discontinuity designs: A guide to practice.

三、如何评价Chen,  Ebenstein, Greenstone & Li（2013）?

 进入正题。我们如何来评价CEGL(2013)的文章呢？

首先，我们要来看看这篇文章的前身，即Douglas, Chen, Greenstone & Li (2009)发在AER上的堪称RDD的典范的经典文章[3]。 

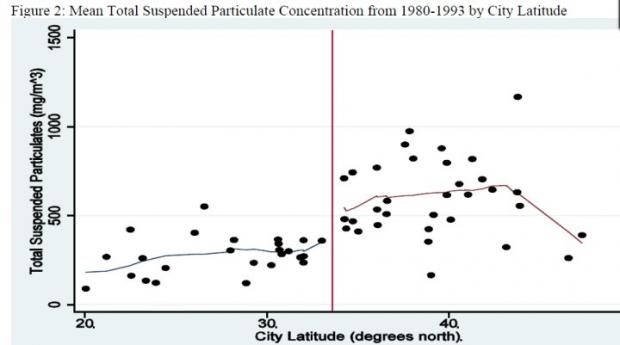
图 1DCGL(2009) 淮河和悬浮物浓度散点图

图1的横轴是城市纬度（红线是秦淮线），纵轴是悬浮物(TSP)浓度。这张图令人信服地指出了悬浮物的浓度在秦淮线附近（秦淮线为红线）有一个很大的跳跃。从图1中目测，比较组划界在1-10度之内估计都没有不会影响结论。北纬40度是什么概念呢？大概就是北京附近。但是这篇文章也就到此为止了。他们既没有讨论悬浮物密度(TSP)和疾病的关系，也没有做任何的“整个北方”的外推。

CEGL(2013)在DCGL（2009）的基础上又前进了一步。他们希望把悬浮物颗粒数和健康状况联系起来。

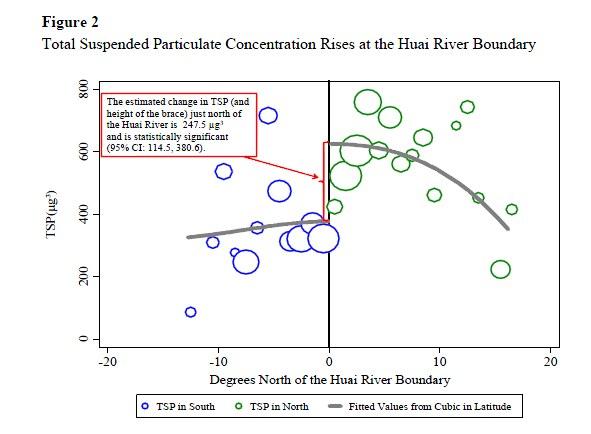
图 2CEGL（2013）淮河和TSP浓度

图2是DCGL(2009)图1 的改进版。横坐标换为距秦淮线的距离，中间0度是秦淮线，纵坐标还是悬浮物密度；圈的大小代表了城市人口的多少。so far so good。

图3是CEGL(2013)的新成就，即统计了各个城市的人均寿命。从图上可以看到，人均期望寿命在秦淮线附近也出现了明显的跳跃。虽然作者们做了许多计量工作，但实际上供暖政策导致减寿5.5年从张图上可以看得八九不离十了。

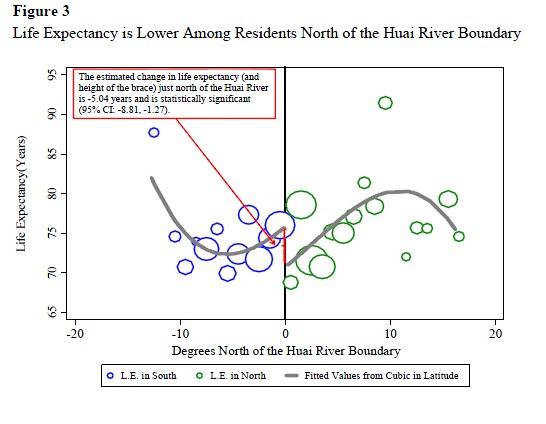
图 3CEGL（2013）淮河和人均寿命

那么RDD的两个软肋CEGL（2013）加固了么？

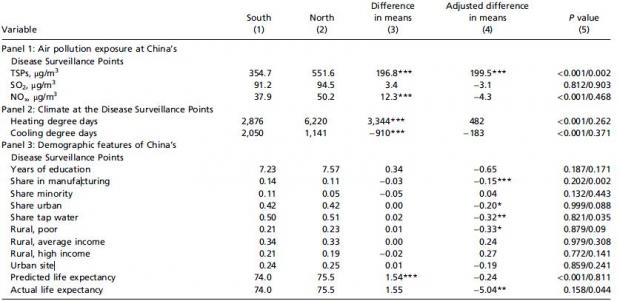
第一条软肋，即混淆变量的同分布，CEGL（2013）做的差强人意。他们控制了一些天气因素和经济因素，但是控制的不是非常好。首先，秦淮河作为分界线不是随机的；中国的气候和植被在秦淮河两岸出现了自然的分野，也就是说自然变量在间断点两端出现了跳跃；而作者并没有详细说明为什么这不重要，或者为什么只控制气温就可以把这些自然变量全部控制住（chenqi，2013）[4]。其次，图3显示了收入对于预期寿命的影响，例如秦淮线左边是江苏上海浙江，图右侧中间凸起处估计是北京周边（但是北京在哪儿？）。因此，我们有理由相信经济发展水平在秦淮线两边也存在巨大差异。然而，让人诧异的是，作者并没有使用GDP或者GNP这样的宏观经济变量，而是使用制造业比重，城市户口比例，以及农村收入的三个离散变量（低收入、中等收入和高收入）作为经济变量。从我的个人经验来看，这些变量是很糟糕的GDP替代品，因为它们的差异太小，完全无法正确反映不同城市间的经济水平差异。CEGL的汇总统计表也证实我的担心，不论是比较样本均值或者条件样本均值，这些变量在南北几乎毫无差异。尽管我们不知道在间断点附近这些指标是否也不存在差异，但是作者不用GDP或者GNP的决定是让人费解的。

就这点而言，我个人怀疑5.5年的估计值可能过高了。

第二条软肋，即边界选择问题，CEGL（2013）可以操作的区间比较小。因为他们的样本容量太小，如果取得太近，标准误会很大。他们把边界定在5°（大约是比较秦淮线两岸各500公里的区域），尽管已经有些夸张，但依然在可以理解的范围内。

但是他们居然把从秦淮线5°内得到的结果外推到整个北方，这就犯了RDD的大忌。作者连间断点附近混淆变量是否相同都尚未说服我，更遑论外推到秦淮线以北所有地区了。特别的，从图3可以看到，秦淮线左右5°内的平均寿命差距是最大的。如果我们只是简单的把这个估计量乘以北方人口，那么其实我们是假设取暖政策造成的健康损害在整个北方都是均质的：即一旦没有了取暖政策，预期寿命曲线要整体上移5.5年。这又是一个很难捍卫的假设。如果这个暗含假设不成立，那么即使秦淮线左右的点估计是无偏的，向整个北方外推的估计量是有偏误的。尽管从逻辑上无法排除低估的可能性，但是从图3来看，我个人觉得高估的可能性要大得多。

 所以，综上所述，我个人的意见是，CEGL(2013)对于取暖政策在秦淮河两岸的健康危害可能有高估，而将之外推到整个北方是很不靠谱的。